Breakwater

This puzzle relies on a few simple physical relations: a) that the flow rates of the various pipes coming from a single tank will be proportional to the cross-sectional areas of the pipes, b) that the sum of all the flow rates entering a tank must equal the sum of all the flow rates exiting a tank, c) that the mixed temperature in any tank is the weighted average of the temperatures entering the tank, and d) that the temperature of all streams leaving the tank are equal to the temperature in the tank.  Once you're past that point the rest is math and logic, as follows.

First the numbering convention: I've assigned each tank a number from left to right, top to bottom.  12 will refer to the tank numbered 12; 12-24 will refer to the pipe running from tank 12 to tank 24. Because I personally find it is the easiest way to visualize and follow the math, I will express the flow of all pipes or the total flow into all tanks in the form X/Y where X is the flow rate in gpm originating from the hot inlet and Y is the flow rate in gpm originating from the cold inlet (think of it as conservation of mass of cold and hot water).  Expressed in this manner the temperature is a simple calculation at any point in the process.

Due to the relation between a small copper and a steel pipe, 1-2 must flow at 12/0, 15/0, or 20/0 and 3-2 must flow at 0/12, 0/15, or 0/20.  Only one combination of these yields a temperature between 110 and 120, and that is if 1-2 has a flow rate of 12/0 and 3-2 has a flowrate of 0/15 (temperature 111.9).  This also means that 2-7, 2-16, and 2-17 all have flow rates of 4/5.

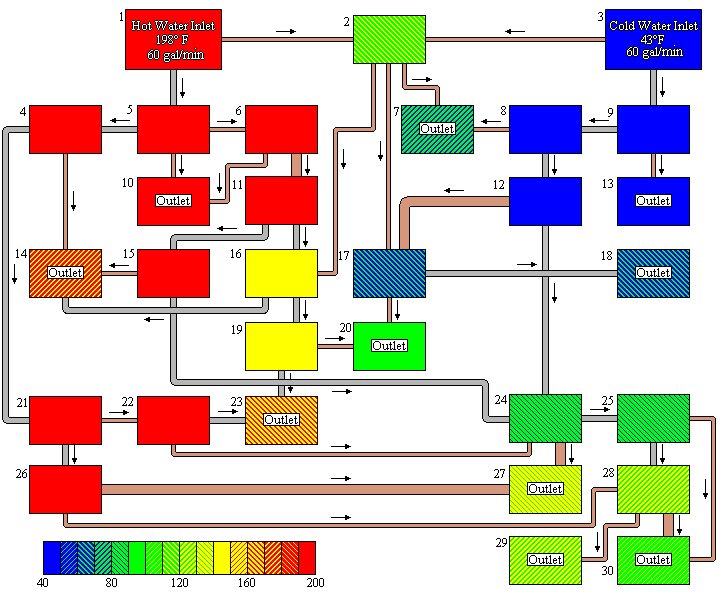
The 48/0 going into tank 5 must come out as either a 12/0, 12/0, 24/0; or an 8/0, 8/0, 32/0.  5-6 must have a flow rate divisible by 6 in order to split into a small and large copper pipe, therefore it must be the former.  This gives 6-10 as 2/0, 6-11 as 10/0, 5-4 as 24/0, and the outlet at 10 is 14/0.  I hope you're writing all this down.

Of 11-15 and 11-16, one must be 4/0 and the other 6/0.  If 11-16 were 4/0 the temperature of 16 (recall 2-16 is known to be 4/5) would be 138.4, but it must be between 140 and 150.  Therefore 11-16 is the 6/0 and 11-14 is the 4/0.  This gives a temperature of 146.3 in 16.  We can also easily find that 15-14 is 1/0 and 15-24 is 3/0.

4-21 must be either 16/0 or 18/0.  21-26 must divide evenly by 6 and must represent between 2/3 and 4/5 of 4-21, and therefore must be 12/0, making 26-27 10/0 and 26-28 2/0.  21-22 is either 4/0 or 6/0, and therefore 22-24 is either 1/0 or 2/0.

Now let's jump to the cold side for a bit.  9-8 can be 0/30 or 0/36.  If it is 0/30, 8-7 can be 0/6 or 0/10.  0/6 would not cool the water in 7 below 80 degrees.  If it were 0/10 then the contents of 12 would be 0/20, which is impossible because the outgoing pipes indicate that it must be divisible by 7, 8, or 9.  Therefore, 9-8 is 0/36 and 9-13 is 0/9.

8-12 can be 0/24 or 0/27.  In either case, 12-17 is 0/15.  12-24 could be either 0/9 or 0/12.  Therefore the composition of 24 can be 4/9, 4/12, 5/9, or 5/12.  4/9 and 5/9 would both be above 90 degrees and 5/12 would be impossible to split into two pipes, ergo it must be 4/12.  Working backwards from here we can get 12-24 is 0/12, 8-7 is 0/9, 22-24 is 1/0, 21-22 is 4/0, and 4-21 is 16/0.

The only way to split 24 is if 24-27 is 2.5/7.5 and 24-25 is 1.5/4.5.  Note that these are still integer flow rates when you take the total quantity of water flowing.  25-30 must be 0.5/1.5 and 25-28 is 1/3 (total composition of 28: 3/3).  This makes 28-30 2.5/2.5 for a total 3/4 in 30, and .5/.5 for 29.

17-20 could be 1.33/6.67 or 1/5.  16-19 could be 3.33/1.67, 4/2, 6/3, or  6.67/3.33.  Therefore 19-20 could be 0.67/0.33, 1.33/0.67, or 2/1.  None of these achieve a temperature greater than 90 degrees with 1.33/6.67, so 17-20 must be 1/5 and 17-18 is 3/15.

Only 2/1 can combine with 1/5 to give a temperature above 90 degrees, so 19-20 is 2/1.  Working backward we find 16-19 is 6/3 and 16-14 is 4/2.

In summary, the outlet flow rates from cold to hot are 0/9, 3/15, 4/14,  3/6, 3/4, 0.5/0.5, 12.5/7.5, 7/2, 13/2, 14/0.  Total water outlets in gpm are 9, 18, 18, 9, 7, 1, 20, 9, 15, 14.  Using A=1, B=2 etc. the answer is IRRIGATION.